Ang mga figure na ginawa mula sa papel ay maaaring magkakaiba.. Gayunpaman, kadalasan ang kagustuhan ay ibinibigay sa mga geometric na hugis. Ang isa sa mga ito ay ang icosahedron (isang pattern para sa gluing), na maaaring tawaging parehong kumplikado at simple sa parehong oras. Kumplikado dahil marami itong mukha – 20 piraso, at mas marami pa itong gilid – 30 piraso. Simple dahil ito ay ganap na simetriko sa gitna nito.
Paglalarawan ng figure
Ang icosahedron (ang pattern para sa gluing ay ibinigay sa ibaba sa artikulo) ay isang figure na nakuha ang pangalan nito mga 100 taon na ang nakalilipas. Ito ay nagmula sa sinaunang Greek numeral na "ikosi", na isinasalin bilang "20". Ang ibang bahagi ng pangalan ay nagmula sa salitang "hedra", na nangangahulugang "gilid". Lumalabas na ang pangalan ay maaaring isalin mula sa Greek bilang "20-sided".
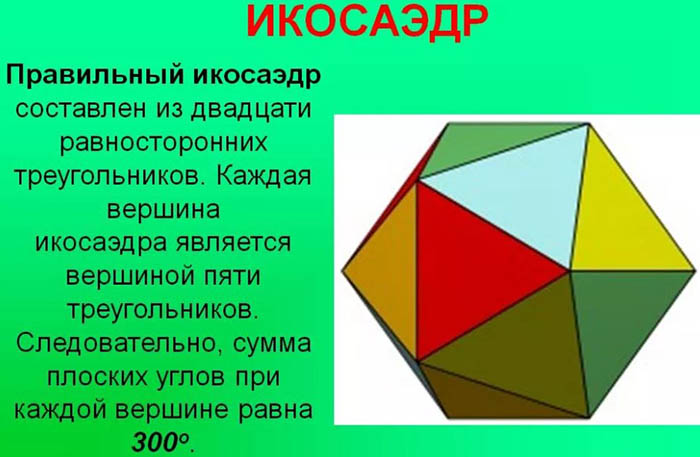
Upang ang isang three-dimensional na geometric na katawan ay tinatawag na isang regular na icosahedron, dapat itong matugunan ang mga sumusunod na kondisyon:
- dapat mayroon itong eksaktong 20 mukha (hindi hihigit at hindi bababa);
- bawat isa sa mga mukha na ito ay dapat na isang regular na tatsulok. Sa geometry, ang isang tatsulok ay tinatawag na regular kung ang lahat ng mga anggulo nito ay pantay. Ang bawat anggulo ng tatsulok na ito ay may halaga na 60 degrees.
Ang icosahedron ay isang regular na polyhedron at isa sa limang tinatawag na "Platonic" solids.
Ang iba pang mga katangian nito ay ang mga sumusunod:
- ang bilang ng mga gilid ng bawat isa sa 20 mukha ay 3;
- bilang ng mga vertex (mga punto ng koneksyon ng mga gilid ng mga mukha) - 12;
- ang bilang ng mga gilid (mga gilid ng mga mukha) na nagtatagpo sa bawat tuktok (punto) ay 5;
- kabuuang bilang ng mga buto-buto - 30;
- bilang ng symmetry axes - 15;
- bilang ng mga eroplano ng mahusay na proporsyon - 15.

Gayunpaman, ang lahat ng mga katangiang ito ay sumusunod mula sa dalawang pangunahing mga nabanggit sa itaas. Kung ang isang figure ay may 20 mukha at kung ang bawat mukha ay isang regular na tatsulok, kung gayon ito ay magiging isang tunay na regular na icosahedron kasama ang lahat ng mga katangian nito.
Ang icosahedron (ang pattern para sa gluing ay hindi mahirap kahit para sa mga nagsisimula) ay isang figure na ang lugar ay madaling matukoy, sa kabila ng malaking bilang ng mga mukha. Bilang karagdagan, maaari itong ilarawan bilang isang sweep area. Kung ang lugar ng 1 sa 20 triangles na mga mukha ng figure ay kilala, kung gayon ito ay sapat na upang i-multiply ang numerong ito sa 20.
Halimbawa, kung ang lugar ng bawat tatsulok ay 4 sq. cm, kung gayon ang kabuuang lugar ng lahat ng mga ibabaw ng icosahedron ay magiging katumbas ng 80 sq. m. Upang gawin ito, dapat na i-multiply ang 4 sa 20.
Mga pangunahing uri
Ang icosahedron na maaaring gawin mula sa papel ay maaaring iba.
Halimbawa, kung:
- Kung gumamit ka lamang ng isang kulay ng papel sa iyong trabaho, ang pigura ay magiging isang kulay;
- ito ay magiging kulay na papel, maaari kang gumawa ng isang multi-kulay na icosahedron, na maglalaro ng iba't ibang kulay at mas maganda ang hitsura.
Kadalasan ang isang icosahedron ay ginawa, na mukhang isang bola ng soccer sa kulay, na may mga puting tatsulok na kahalili ng mga itim. Sa katotohanan, hindi ito magiging bola, dahil malayo ito sa pag-ikot. Ang mas mahirap isagawa ay ang icosahedron, na may hugis ng isang bituin. Mayroon nang mga facet dito na namumukod-tangi laban sa background ng iba.
Ang pinakamaganda ay ang icosahedron, na pinalamutian ng iba't ibang pandekorasyon na elemento. Ang mga ito ay maaaring maging anumang mga dekorasyon: isang bagay na makintab, maliwanag - isang bagay na madaling nakakabit sa ibabaw ng papel. Ang icosahedron na ito ay maaaring gamitin bilang laruan ng Bagong Taon at isabit sa Christmas tree.

Mayroong hindi mabilang na icosahedra sa geometry. Ang ilan sa kanila ay may higit na simetriko, habang ang iba, sa kabaligtaran, ay hindi gaanong simetriko. Ang pinakakaraniwan ay ang regular na icosahedron - ang isa na may eksaktong 20 magkaparehong mukha. Sa matematika, ang isang regular na icosahedron ay maaaring tawaging alinman sa isang convex o isang non-convex na katawan.
Sa anumang kaso, ang bawat isa sa kanila ay may 20 mukha at 1.5 beses na higit pang mga gilid. Parehong may tinatawag na ixosahedral symmetry. Gayunpaman, kadalasan ay ang convex form na tinatawag na regular na icosahedron, habang ang non-convex form ay nabibilang sa kategorya ng mahusay na icosahedra.
Ang icosahedron (scan para sa gluing) ay maaaring katawanin ng mga sumusunod na opsyon:
| Pigura | Paglalarawan |
| Matambok na icosahedron | Mayroon itong 20 mukha at 12 vertex. Ang geometric solid na ito ay may dual polyhedron. Ito ay tinatawag na isang regular na dodecahedron. Mayroon itong 3 regular na 5-sided na mukha sa paligid ng bawat vertex. |
| Mahusay na icosahedron | Mayroon itong eksaktong 20 mukha, bawat isa ay isang regular na tatsulok. Gayunpaman, ang tuktok nito ay hindi isang 5-gon, ngunit isang pentagram. Ito ay para sa kadahilanang ito na ang mga gilid ay bumalandra sa geometrically. Kapag nagsalubong sila, walang nabuong mga bagong gilid. Ang dual polyhedron ng dakilang icosahedron ay ang dakilang dodecahedron. Mayroon itong 3 mukha na nakatutok sa paligid ng bawat vertex, na ang bawat isa ay isang 5-gon. |
| Stellated icosahedra | Kung ang mga mukha o gilid ng isang polyhedron ay lumawak, pagkatapos ay kapag hinawakan nila, isang hugis ng bituin ay nabuo. Nangyayari ito nang simetriko, kaya ang resultang katawan ay may parehong mga simetriko gaya ng orihinal na mga figure. Ang siyentipikong gawain ng Coxeter na "59 icosahedra" ay naglilista ng halos 60 stellated na uri ng polyhedra na ito. Marami sa kanila ay may hiwalay na facet sa bawat isa sa 20 eroplano. Maraming iba pang mga katawan ang may higit sa 1 mukha sa eroplano. Maaari silang mabuo sa pamamagitan ng pagsasama ng mas simpleng polyhedra. |
| Pseudoicosahedron | Isang regular na icosahedron na baluktot, na nagiging sanhi ng pagbabawas ng simetrya nito. |
| Ang icosahedron ni Jessen | Kung ang isang three-dimensional na geometric na katawan ay may 12 mga mukha, ang bawat isa ay isang isosceles triangle, at ang mga mukha na ito ay nakaayos sa paraang bumubuo sila ng isang non-convex na katawan, kung gayon ang figure na ito ay tatawaging Jessen icosahedron (o orthogonal icosahedron). Mayroon itong tamang 2-panig na anggulo. Ang isa sa mga tampok nito ay na ito ay equidecomposable na may isang heksagono, ang bawat mukha nito ay isang parisukat. Nangangahulugan ito na maaari itong hatiin sa maliit na polyhedra, at pagkatapos ay ginagamit upang bumuo ng isang heksagono na may pantay na laki ng mga mukha. Ang gayong heksagono ay isang kubo. |
Paano gumawa ng isang regular na icosahedron sa labas ng papel?
Ang pag-unlad para sa gluing ng Icosahedron para sa pagmamanupaktura ay mangangailangan ng paghahanda ng mga sumusunod na materyales at tool:
- papel. Maaari itong corrugated, puti, o kulay. Ang density nito ay maaari ding mag-iba;
- gunting. Kinakailangan para sa pagputol ng mga figure ng mga kinakailangang laki at hugis;
- pandikit. Ang pinakamahusay na pagpipilian ay regular na PVA, dahil nangangailangan ng mahabang panahon upang matuyo, na sapat upang maalis ang mga posibleng error;
- tagapamahala. Kung wala ito, magiging napakahirap na ibaluktot ang papel nang pantay-pantay sa linya ng fold.

Maaari ka ring gumamit ng mga karagdagang materyales upang palamutihan ang iyong papel na gawa. Ito ay isang bagay ng panlasa at imahinasyon.
Pagkatapos ihanda ang lahat ng mga materyales at tool, maaari kang magpatuloy nang direkta sa proseso ng creative.
Ang gawain ay nagaganap sa mga sumusunod na yugto:
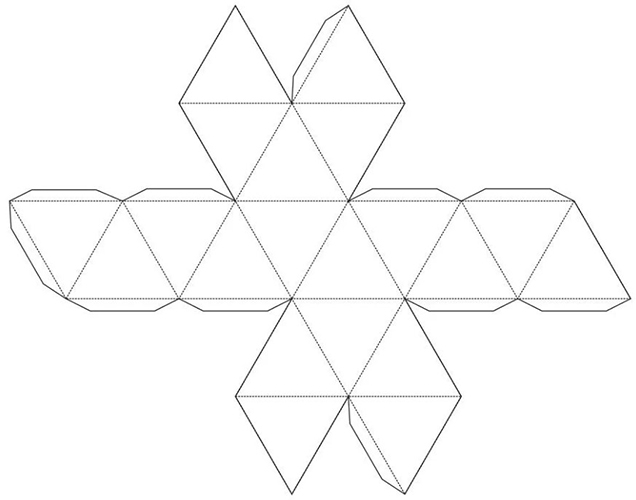
- I-print ang natapos na template sa isang printer at ilipat ito sa inihandang materyal. Dapat mag-ingat kapag naglilipat. Kung hindi man, ang mga marka ay hindi tama, na nangangahulugan na ang figure sa kabuuan ay magiging hindi pantay o wala sa lahat. Ito ay lubos na inirerekomenda na gumamit ng isang ruler.
- Simulan ang pagputol ng template. Ang gunting ay dapat na mahigpit na dumaan sa mga tuldok na linya. Kung hindi man, hindi posible na idikit ang lahat ng mga elemento ng figure nang magkasama. Gayunpaman, hindi ka dapat magmadali, dahil ang template ay madaling masira ng walang ingat na paggalaw. Mahalaga na ang lahat ng triangular na elemento ng template ay may pantay na panig. Ito ay isa sa mga pangunahing katangian ng icosahedron. Ito ay kasinghalaga at obligado ng kondisyon na ang lahat ng panig ng parehong parisukat ay palaging pantay. Kung ang panuntunang ito ay nilabag, ang pagkakaiba sa pagitan ng mga panig ay magiging kapansin-pansin.
- Pagkatapos putulin ang blangko, simulan ang baluktot ang pigura. Talagang kailangan ng ruler dito. Ang mga fold point ay ipapakita bilang mga solidong linya, at ang gluing ay dapat gawin kasama ang mga tuldok na linya. Ang pangunahing layunin ay upang ikonekta nang tama ang lahat ng mga mukha ng mga triangular na elemento ng figure. Kung sa ilang kadahilanan ay wala kang pandikit na PVA, at sa halip ay nakahanap ka ng isang mabilis na pagkatuyo na pandikit, dapat mong tandaan na walang puwang para sa pagkakamali. Kung hindi mo ikinonekta nang tama ang mga bahagi at ang pandikit ay natuyo sa loob ng ilang segundo, hindi na posibleng paghiwalayin ang mga elemento. Kung nagtatrabaho ka sa PVA glue, kakailanganin mong pindutin nang husto ang bawat joint. Pagkatapos ilapat ang pandikit, panatilihing nakadikit ang mga bahagi sa isa't isa nang mga 20 segundo.
- Palamutihan ang tapos na produkto. Para sa mga ito maaari mong gamitin ang mga pintura, marker, lapis, pastel. Maaari ka ring mag-attach ng thread sa natapos na figure upang ma-hang ito. Kadalasan ang gayong mga likhang papel ay ginagamit bilang isang dekorasyon ng Christmas tree para sa Bagong Taon.
Ang paggamit ng icosahedron ay maaaring iba. Maaari itong gumanap hindi lamang isang aesthetic kundi isang praktikal na function.
Maraming kulay na icosahedron
Ang icosahedron (ang pattern para sa gluing ay maaaring kulay) na maraming kulay ay maaaring maging isang magandang visual aid kapag nag-aaral ng mga kulay na kulay kasama ang mga bunsong bata.
Upang magtrabaho sa paglikha ng isang multi-kulay na icosahedron, kakailanganin mo ang mga sumusunod na materyales at tool:
- yari na template (madaling mahanap sa Internet);
- may kulay na papel (kung wala ka, maaari mong kulayan ang puting papel na may mga panulat, pintura o lapis, na magiging kawili-wili at nakakaaliw para sa mga bata);
- pandikit (inirerekumenda na gumamit ng matagal na pagpapatayo ng PVA);
- gunting.
Kapag handa na ang lahat, maaari kang magpatuloy nang direkta sa proseso ng paglikha, na binubuo ng mga sumusunod na yugto:
- Gumawa ng blangko gamit ang isang stencil. Kung tungkol sa bilang ng iba't ibang kulay, maaari itong maging anuman sa pagpapasya ng taong gumagawa ng craft. Gayunpaman, mas maraming iba't ibang maliliwanag na kulay ang mayroon, mas magugustuhan ng bata ang produktong ito. Maaari mong kunin, halimbawa, ang mga pangunahing kulay ng bahaghari. Maaari kang magdagdag ng ilang higit pang mga kulay o, sa kabaligtaran, alisin ang mga tila hindi kailangan (halimbawa, hindi kinakailangan para sa isang figure na magkaroon ng parehong asul at mapusyaw na asul).
- Ikonekta ang lahat ng mga elemento gamit ang long-drying PVA glue.
Stellated icosahedron
Ang stellated icosahedron ay isa sa pinakamahirap gawin. Gayunpaman, ang buong kahirapan ay nakasalalay sa katotohanan na kailangan mong magkaroon ng maraming pasensya. Ang trabaho ay aabutin ng maraming oras.
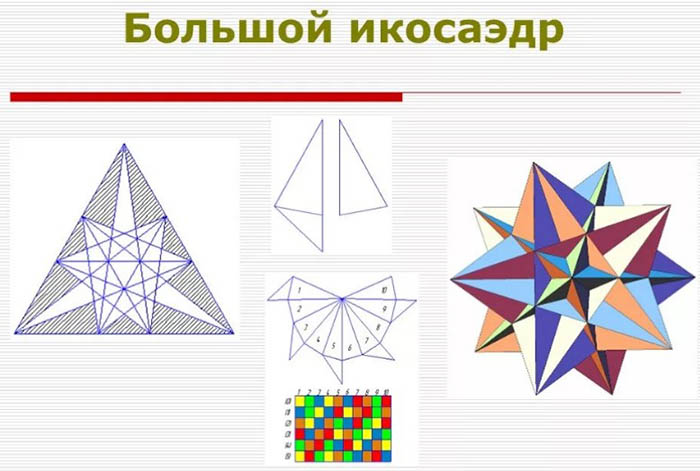
Bilang karagdagan sa pasensya, kailangan mo:
- gunting;
- may kulay na papel;
- pandikit.
Maaari kang maghanda ng ilang mga pandekorasyon na elemento upang palamutihan ang tapos na produkto. Ang mga ito ay maaaring maging anumang mga bagay na mukhang maganda: may kulay na mga thread, ribbons, malagkit na kuwintas.
Kapag naihanda na ang lahat ng kailangan, maaari kang magpatuloy nang direkta sa proseso ng paglikha, na binubuo ng mga sumusunod na yugto:
- Gumupit ng 30 parisukat mula sa papel na may mga gilid na 5 cm bawat isa. Ang bawat parisukat ay dapat na may sukat na 25 sq. tingnan. Sa kasong ito, dapat mong gamitin ang papel na may 3 kulay. Maaari itong maging anumang mga tono, halimbawa, berde, asul at pula. Sa dulo dapat mayroong 10 parisukat ng bawat kulay.
- Kapag ang kinakailangang bilang ng mga parisukat ay naputol, maaari mong kunin ang isa sa mga ito at tiklupin ito sa kalahati. Pagkatapos ang bawat kalahati ay kailangang baluktot patungo sa gitna, ituwid at ang mga kabaligtaran na sulok ay nakatiklop nang dalawang beses.
- Gawing parang klasikong tik ang papel sheet, na kadalasang gawa sa papel. Upang gawin ito, tiklupin ang malaking sulok mula sa ibabang bahagi.
- Hawakan ang kabilang panig ng parisukat. Dapat itong baligtarin, pagkatapos ay dapat na nakatiklop ang tuktok na bahagi upang bumuo ng isang sobre. Sa kasong ito, ang matinding anggulo nito ay dapat na maipasok sa loob ng produkto.
- Magpatuloy sa pagtatrabaho sa unang parisukat. Ngayon na ito ay naging isang sobre, kailangan mong tiklupin ito sa kalahati at tiklupin ang mga nakausli na tainga, na idirekta ang mga ito sa mga panlabas na sulok ng mga tatsulok. Susunod, pagkatapos ng pagtuwid, isang yunit ng pagpupulong ay nabuo.
- Upang magawa ang pinakamahabang bahagi ng trabaho, ang lahat ng 5 hakbang na inilarawan sa itaas ay dapat na ulitin sa bawat isa sa 29 na natitirang mga parisukat. Mangangailangan ito ng maraming pasensya. Maaaring hindi posible na gawin ang lahat ng 30 kinakailangang modelo nang sabay-sabay. Inirerekomenda na magpahinga mula sa malikhaing prosesong ito.
- Kapag handa na ang lahat ng 30 bahagi, maaari mong kunin ang isa sa mga ito at itulak ang dulo nito sa bulsa ng isa pa (kinakailangang may ibang kulay). Alinsunod dito, ang sulok ng elementong ito ay dapat magkasya sa bulsa ng ikatlong bahagi, na naiiba sa kulay mula sa iba pang dalawa. Ang sulok ng ika-3 piraso ay dapat magkasya sa bulsa ng ika-4 na piraso, na magiging kapareho ng kulay ng unang piraso. Sa ganitong paraan ang mga kulay ay maghahalili.
- Ipasok ang dulo ng ika-3 piraso sa ika-2 piraso. Ang unang bahagi ay ipinasok dito, at ang dulo ng ikalawang bahagi ay inalis sa bulsa ng unang link.
- Ipasok ang 2nd puzzle sa ika-3, pagkatapos ay ang 1st sa loob nito, at ang buong bagay ay sarado sa ika-3.
- Ipunin ang lahat ng mga elemento ayon sa diagram sa itaas. Kapag ang huling elemento ay nasa lugar, ang mahaba at maingat na gawain ng paggawa ng stellated icosahedron ay maaaring ituring na kumpleto.
Pandekorasyon na icosahedron
Ang 20-sided na geometric na katawan na ito na gawa sa papel gamit ang kusudama technique ay magiging maganda sa isang festive tree sa Bisperas ng Bagong Taon. Upang makagawa ng isang pandekorasyon na icosahedron, kailangan mong gupitin ang 30 mga parisukat mula sa papel. Pinakamainam kung ito ay mapusyaw na dilaw.

Ang pagkakaroon ng paghahanda ng kinakailangang bilang ng mga parisukat ng papel, maaari mong simulan ang proseso ng malikhaing:
- Kunin ang isa sa mga parisukat (lahat sila ay pareho, kaya maaari kang kumuha ng alinman), tiklupin ito sa kalahati, at ibaluktot ang mga gilid sa gitna.
Pagkatapos ang workpiece ay buksan at pagkatapos ay nakatiklop sa gitnang linya. Ang mga gilid ay kailangang nakatiklop patungo sa gitna at pagkatapos ay buksan muli. - Baluktot ang piraso upang ang parisukat ay maging isang tatsulok. Pagkatapos nito, dapat itong ituwid at ang mga bahagi ng gilid ay baluktot patungo sa gitnang linya. Pagkatapos ang isa sa mga ilalim na gilid ay dapat na nakatiklop sa gilid. Ang resulta ay dapat na isang sulok. Ang kabaligtaran na gilid ay kailangang nakatiklop patungo sa gitna upang bumuo ng isang matangos na ilong.
- Ulitin muli ang buong pamamaraan sa itaas, ngunit ngayon sa ika-2 bahagi ng bahagi. Ang resulta ay isang parisukat na may isang pares ng hugis tatsulok na mga spout.
- Ang puzzle ay kailangang nakatiklop nang pahaba, kung saan ang isa sa dalawang tatsulok ay nakatiklop pasulong at ang isa ay nasa tapat na direksyon.
Susunod, ang bahagi ay kailangang ituwid. Upang gawin ito, kailangan mong hilahin ang mga dulo nito. Ito ay lilikha ng unang link ng pandekorasyon na icosahedron. Gayunpaman, dapat mayroong 30 tulad na mga link sa kabuuan, kaya ang pamamaraan ay isinasagawa ng 29 na beses. - Kapag handa na ang lahat ng 30 elemento, maaari mong simulan ang pagkonekta sa kanila. Ginagawa ito bilang mga sumusunod: ang dulo ng isang link ay dapat na ipasok sa bulsa ng isa pa; pagkatapos ay ang dulo ng ika-3 link ay ipinasok sa parehong bulsa; at ang dulo ng ika-4 ay sinulid hanggang sa ika-5; pagkatapos ay ang 1st ay ipinasok sa ika-5, na nagreresulta sa isang saradong singsing.
- Ang lahat ng mga tip ng susunod na talulot ay kailangang ilagay sa mga puwang sa pagitan ng mga link upang bumuo ng isang tatsulok.
- Ang bawat bahagi ay dapat sumailalim sa isang katulad na pamamaraan. Matapos isara ang huling tatsulok, nabuo ang isang magandang pigura na magiging maganda sa holiday tree.
Ang pagkakaroon ng naiintindihan kung paano gumawa ng isang pattern ng papel para sa gluing isang icosahedron, maaari mong simulan ang modelo ng iyong sarili, gamit ang iba't ibang mga solusyon sa kulay, materyales at dekorasyon.
Video tungkol sa paggawa ng isang icosahedron mula sa papel
Master class sa paggawa ng icosahedron na may mga butas:
